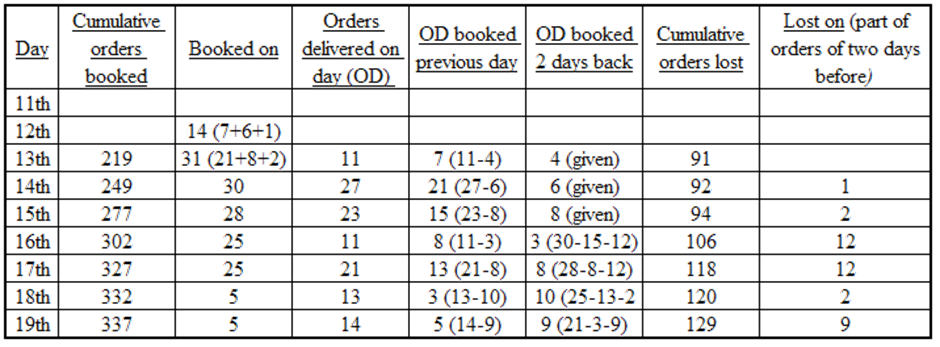
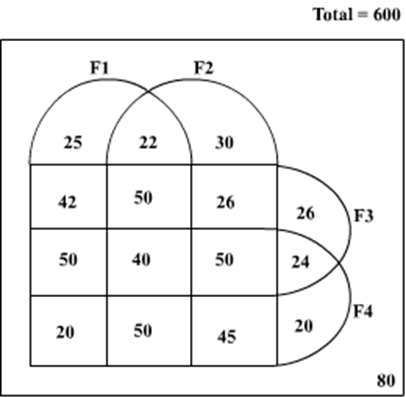
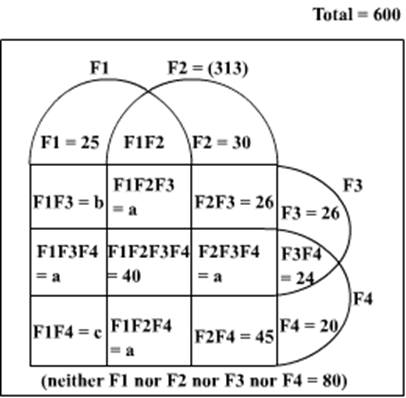
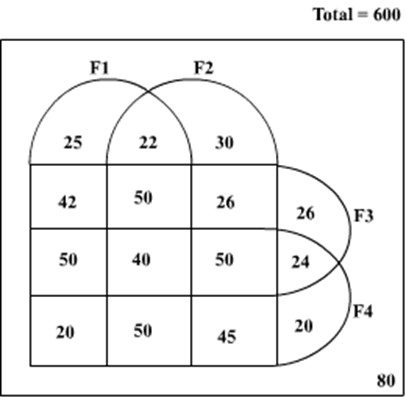
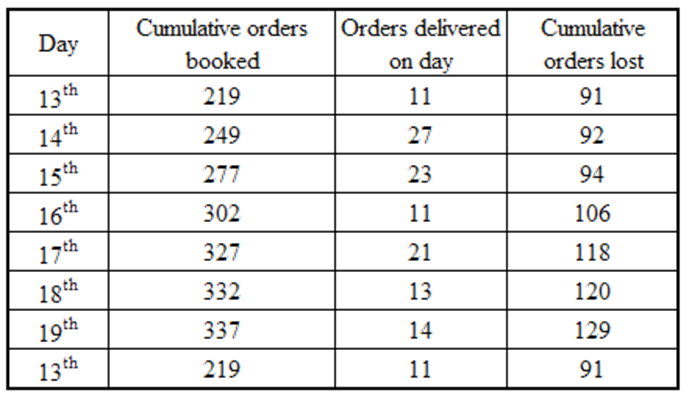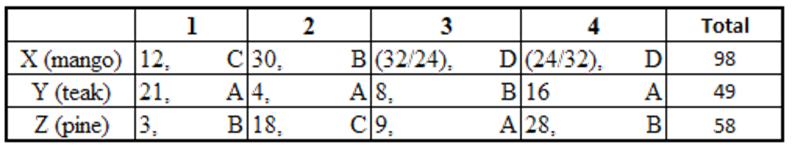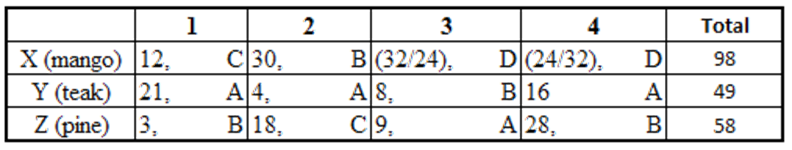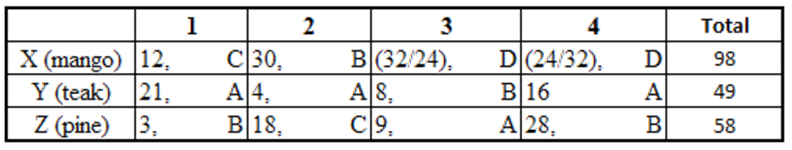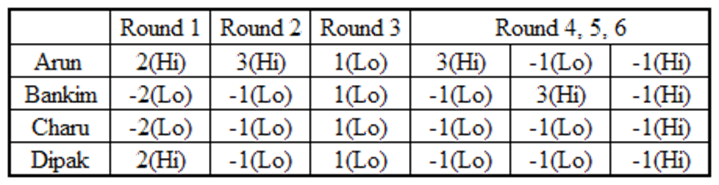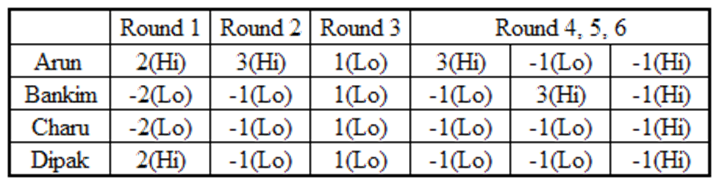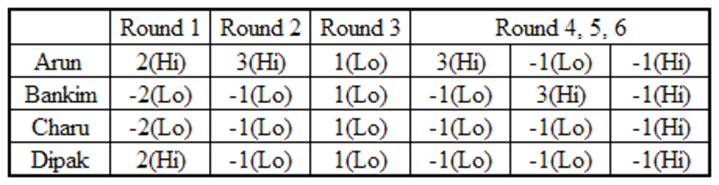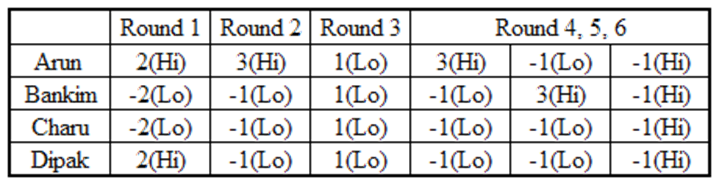The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
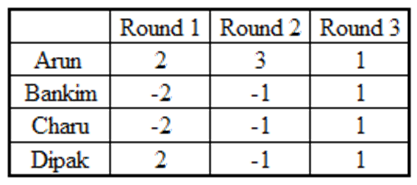
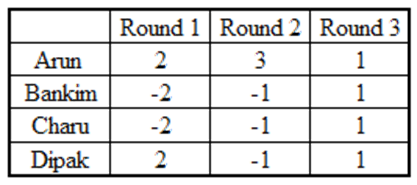
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
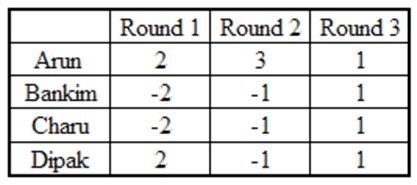
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
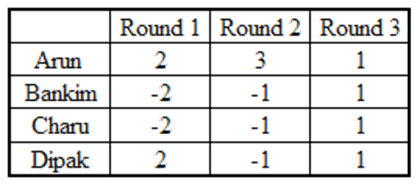
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
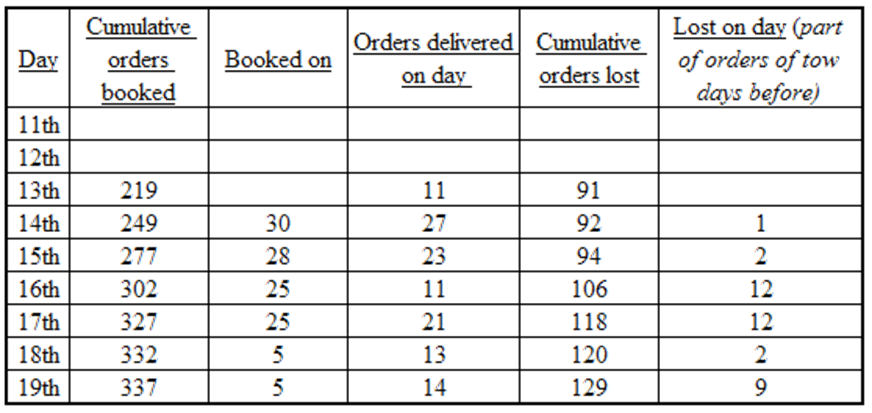
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
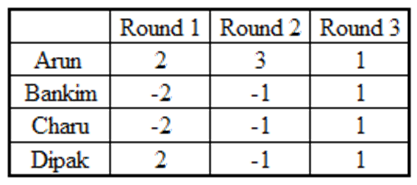
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
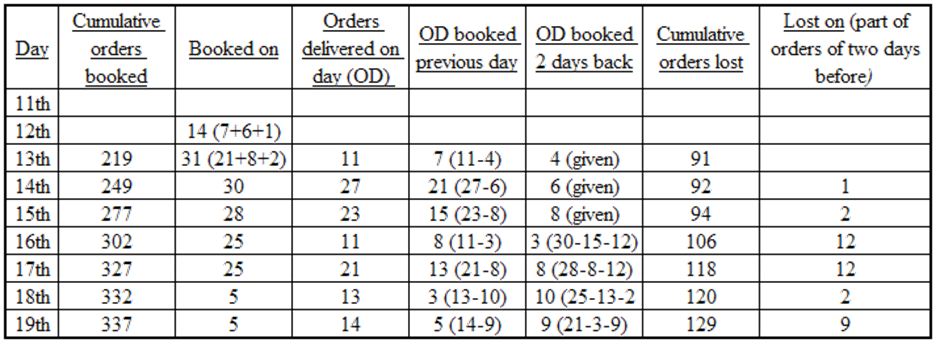
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo.
If all four bid Hi, each gets – 1. In this case, total points in the round = – 4.
If three Hi and one Lo, each Hi gets +1, the Lo gets –3. In this case, total points in the round = 0.
If two Hi and two Lo, each Hi gets +2, each Lo gets –2. In this case, total points in the round = 0.
If one Hi and three Lo, the Hi gets +3, each Lo gets –1. In this case, total points in the round = 0.
If all four bid Lo, each gets +1. In this case, total points in the round = + 4.
From fact (1), the total points of the first 3 rounds together add up to + 4 (6–2–2+2). And we know that each round’s total can be either – 4 or 0 or + 4.
So, one way of achieving + 4 in three rounds is to get + 4 in one round and 0 in other two rounds.
And another way of achieving + 4 in three rounds is to get + 4 in two rounds and – 4 in one round.
But in the latter case, every player will get either + 1or – 1 in each of the first three rounds.
i.e., Dipak’s score would be equal in at least two rounds,which is not possible by fact (3).
i.e., in the first three rounds, the totals were +4, 0, 0 in some order.
When the total was + 4, every player scored 1 point. As Arun had scored 6 points at the end of the third round, he must have scored 3 and 2 in two rounds in some order.
When Arun scored 3 points, each of the remaining players scored –1 point. Now we know score of each player in two rounds (out of the first three rounds).
Arun = 3 + 1 = 4, Bankim = – 1 + 1 = 0, Charu = – 1 + 1 = 0, Dipak = – 1+1 = 0
So in the round when Arun scored 2, Bankim = – 2 + 0 = –2, Charu = – 2 + 0 = –2, Dipak = 2 + 0 = 2
Thus, Dipaks score in the first three rounds would be 2, 1, –1.
Therefore, using fact (3) we can conclude
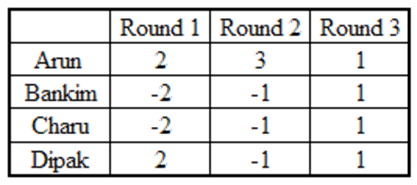
From facts (1) and (2), Arun, Bankim, Chanru and Dipak scored (7 – 1 =) +1, (–1–(–2) =) +1, (–5–(–2) =) –3 and (–1–2 =) –3 points respectively.
So, the total points of the last 3 rounds together addup to – 4 (1+1–3–3).
Now, – 4 = – 4 – 4 + 4 or – 4 + 0 + 0
If the scores of the three players together in the last three rounds are – 4, – 4, and + 4, then each player would have scored –1, –1, +1.
And total points scored by each player would be – 1. But this isnot possible. So – 4 = – 4 + 0 + 0
The total number of points in a round by all the three players would be – 4 only when all the four bid Hi.
Arun had scored 3, 2 and 1 points in first three rounds. Therefore, using fact (4), in the last tworounds also, he must have scored 3 points in exactly one round.
Also, in this round remaining threeplayers have scored – 1 point each. Now we know the scores of the four players in two rounds out ofthe last three rounds.
Arun: 3 – 1 = 2, Bankim = Charu = Dipak = – 1 – 1 = – 2,
So, in the remaining round, points scored by
Arun: + 1 – (2) = –1
Bankim: + 1 – (–2) = 3
Charu: – 3 – (–2) = –1
Dipak: – 3 – (–2) = –1
Therefore, we can make a final table as follows:

Bankim bid Lo in 4 rounds.
Answer: 4.